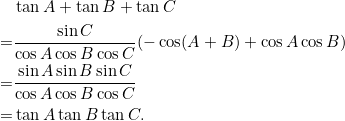I enjoyed proving trigonometric identities when I was in high school. The following identity that appeared on an old mathematics contest (Descartes contest) is perhaps my favourite one as it has a neat formulation:
For triangle ![]() , we have:
, we have:
![]()
Here is the proof:
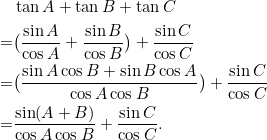
Since ![]() , we have
, we have ![]() . Hence
. Hence
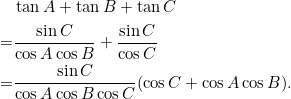
Since ![]() , we have
, we have ![]() Thus
Thus