Mathematical Induction – Peter’s Blog

The Principle of Mathematical Induction is arguably one of the most powerful techniques in mathematics. Formally, the principle asserts the following:

Principle of Mathematical Induction: Consider a set of statements $P(n),$ where $n \in \mathbb{N}$ . Suppose:

$\begin{align*} 1) & \quad P(n) \mbox{ is true for } n=1. \\ 2) & \quad \mbox{If } P(n) \mbox{ is true for } n=k, \mbox{then it is also true} \\ & \quad \mbox{for } n=k+1. \\ \end{align*}$

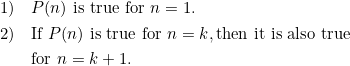
Then $P(n)$ is true for all $n \in \mathbb{N}$ .

To appreciate the principle, let us imagine the following scenario. Consider a monkey resting on the ground with an infinitely tall ladder ahead of him. Suppose there is a banana on one of the rungs of the ladder. How would we guarantee that the banana can be reached?

In fact, the conditions given in the principle of mathematical induction guarantee this. Specifically, the monkey has to be able to get up to the first rung. This amounts to proving $P(1)$ , which is the first condition. Then we need to know that once he is on a rung, he can climb up to the next rung. This amounts to proving that $P(k) \implies P(k+1)$ , which is the second condition. These conditions thus guarantee that the monkey can keep climbing up the ladder and eventually reach a banana on the ladder, no matter how high it was placed originally.

The power of the principle is that the $P(n)$ 's can represent many different sets of statements. One of the applications of this principle is in proving the Marriage Lemma, which will be the subject of a future post.