Marriage Lemma – Peter’s Blog

The Marriage Lemma is a neat result that has the following interesting formulation:

Consider a group of men and women in a party. Suppose in any group of n men, there are a minimum of n women liked by at least one of the men in the group. Then it is possible to match up each man with some woman in the party that he likes such that no two men are paired with the same woman.

A comment is in order. We clearly see that the condition in the lemma is the weakest condition that can be imposed. Indeed, if some group of $n$ men only like at most $n-1$ women, then it is obvious that we cannot pair the men and women as asserted in the lemma. On the other hand, it is not at all obvious that the pairings can occur with the given condition, as the same woman can be liked by two or more men.

The proof of this lemma relies on the Principle of Mathematical Induction in a previous post. In fact, we shall use the strong form of the above principle as follows:

Principle of Mathematical Induction (Strong Form): Consider a set of statements $P(n),$ where $n \in \mathbb{N}$ . Suppose:

$\begin{align*} 1) & \quad P(n) \mbox{ is true for } n=1. \\ 2) & \quad \mbox{If } P(n) \mbox{ is true for all } n \leq k, \mbox{then it is also} \\ & \quad \mbox{true for } n=k+1. \\ \end{align*}$

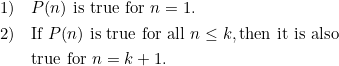
Then it is true for all $n \in \mathbb{N}$ .

It is not difficult to see this if you appreciate the standard form of mathematical induction. Once again, using the monkey example in the previous post, all we are saying now is that if the monkey can climb the first step, and we know that whenever the monkey can climb the next step given that it has climbed all the previous steps, then the monkey can climb infinitely high.

Let us now prove the marriage lemma by induction on the number of men, which we will denote by $m$ .

First, if $m=1$ , then the result is immediate. Indeed, the hypothesis states that this one man likes at least one woman, so we can just pair him up with any one of them.

Hence, suppose that it is true for all $m \leq k$ . Let us prove that when $m=k+1$ , the marriage lemma still holds.

To simplify the exposition, let us denote $\mathcal{M}$ to be the set of these $m$ men and $\mathcal{W}$ be the set of women in the party. For a subset $\mathcal{N} \subset \mathcal{M}$ of men, let $\mathcal{W}(\mathcal{N})$ denote the set of women liked by some member in $\mathcal{N}$ . As is customary in set theory, for any set $\mathcal{S}$ , we let $|\mathcal{S}|$ denote the cardinality (or number of elements) in $\mathcal{S}$ . As well, for sets $\mathcal{A}$ and $\mathcal{B}$ , $\mathcal{A}\backslash \mathcal{B}$ denotes the elements in $\mathcal{A}$ which are not in $\mathcal{B}$ .

We will consider two cases:

Case 1: There exists a subset $\mathcal{N}$ of men, with $|\mathcal{N}|<m$ , such that $|\mathcal{N}|=|\mathcal{W}(\mathcal{N})|$ .

In this case, we apply the induction hypothesis on $\mathcal{N}$ to get a pairing of men and women for the men in $\mathcal{N}$ . For the remaining men, let $\mathcal{S}$ be a subset of them and $\mathcal{W}'(\mathcal{S})$ be the set of remaining women in the party liked by at least one member in $\mathcal{S}$ . It suffices to show that $|\mathcal{S}|\leq |\mathcal{W}'(\mathcal{S})|$ , for then we can apply the induction hypothesis to get a pairing of the men in $\mathcal{M} \backslash \mathcal{N}$ .

Suppose on the contrary, we have $|\mathcal{S}| > |\mathcal{W}'(\mathcal{S})|$ . Notice that

$\begin{align*} |\mathcal{S}\cup \mathcal{N}|& = |\mathcal{S}|+|\mathcal{N}| \\ & >|\mathcal{W}'(\mathcal{S})|+ |\mathcal{W}(\mathcal{N})|\\ & =|\mathcal{W}(\mathcal{S} \cup \mathcal{N})|.\\ \end{align*}$

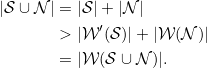
However, this contradicts the hypothesis of the marriage lemma for the set $\mathcal{S} \cup \mathcal{N}$ . Thus $|\mathcal{S}| \leq |\mathcal{W}'(\mathcal{S})|$ and so we are done in this case.

Case 2: For all subset $\mathcal{N}$ of men, with $|\mathcal{N}|<m$ , we have $|\mathcal{N}|<|\mathcal{W}(\mathcal{N})|$ .

In this case, take any one of the men and pair him with some woman he likes. Consider the remaining men. Let $\mathcal{S}$ be a subset of these men. Notice that $|\mathcal{S}|<\mathcal{W}(\mathcal{S}) \leq \mathcal{W}'(\mathcal{S})+1$ . (Here, $\mathcal{W}'(\mathcal{S})$ is defined as in Case 1.) Thus $|\mathcal{S}| \leq |\mathcal{W}'(\mathcal{S})|$ . Hence, we can apply the induction hypothesis to get a pairing for the remaining men in the party.

Thus, the result now follows by induction.