Telescoping series – Peter’s Blog

One of my favourite tricks in mathematical problem solving is the idea of a telescoping series. Consider the following problem:

Find the sum of

$\begin{equation*} \frac{1}{2} + \frac{1}{6} + \frac{1}{12} + \ldots + \frac{1}{n(n+1)}. \end{equation*}$

This seems to lead to an ugly expression without any insights into the problem. But now this is where a beautiful observation comes in:

$\begin{equation*} \frac{1}{m(m+1)}=\frac{1}{m} - \frac{1}{m+1}. \end{equation*}$

This allows us to rewrite our original expression in the form:

$\begin{align*} \left( \frac{1}{1} - \frac{1}{2} \right) & + \left( \frac{1}{2} - \frac{1}{3} \right) + \left( \frac{1}{3} - \frac{1}{4} \right) \\ & + \ldots + \left( \frac{1}{n}-\frac{1}{(n+1)} \right) .\\ \end{align*}$

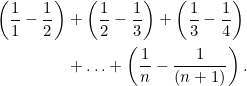
As the above involves only addition and subtraction, we are free to take out the brackets and regroup the terms as follows:

$\begin{align*} \frac{1}{1} &+ \left( - \frac{1}{2} + \frac{1}{2} \right) + \left( - \frac{1}{3} + \frac{1}{3} \right) \\ & + \ldots + \left( -\frac{1}{n} + \frac{1}{n} \right) - \frac{1}{n+1}. \\ \end{align*}$

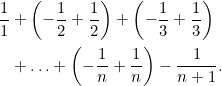
Note the the terms in each bracket sum to 0 so we are left with only the first and last term, so the sum in the original expression is:

$\begin{equation*} 1- \left( \frac{1}{n+1} \right) = \frac{n}{n+1}. \end{equation*}$

The idea of a telescoping series is to expand each summand (using the above observation in our case) from one term to several terms and then to notice that some terms cancel out each other, so that we end up with a tidy expression. The analogy is using the telescope whereby we stretch it out to use it and then collapse it afterwards.