An Insightful Geometry Problem

Calculate the area of the shaded region.

There are many solutions to this problem.  One can divide the shaded region into triangles and sum these areas.  Alternatively, one might deduct the areas of the unshaded triangles from the large rectangle to get the area of the shaded area.  These approaches involve straightforward but tedious calculations.  Here is a solution that avoids many tedious calculations by drawing on two fundamental techniques in geometry: geometric transformations and exploiting symmetry.

Let us shrink the diagram above in the -direction (horizontal direction) by a factor of 2, and label the vertices as below:

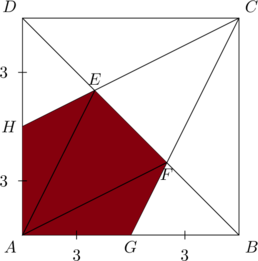
Then the shaded area in this new diagram is half of that in the original diagram.  Let us proceed to calculate this area.  We use the notation to denote the area of the polygon with vertices and to denote the length of the line segment .  Since ,  as the two triangles have the same height.  As well, by symmetry , so .  Hence,

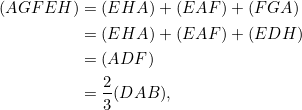
since from similar triangles , so that .  Thus,

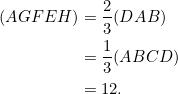
Finally, stretch the modified diagram back by a factor of 2 to conclude that the area of the shaded region in the original diagram is 24.