Applying Modular Arithmetic in Accounting

What does modular arithmetic have anything to do with accounting? I didn't know until this sentence appeared in the textbook of my Grade 10 accounting course:

"In a bank reconciliation, if the two sides don't match, take the difference and see if it is divisible by 9. If it is, then a possible source of error is that an entry is entered into each side but with digits reversed."

Let us understand what we are saying here. The goal of a reconciliation is to ensure that starting from a common balance in an account, the bank entries in that account for a particular month and the book entries for the same account in the same month both lead to a common ending balance. As one can imagine, if there are many entries in the month, possible data entry or omission errors can lead to different balances. In reconciliation, it is important to identify these errors and correct them so that the bank balance matches the book balance.

One of the students raised his hand and asked the teacher why that statement is true. The teacher looked puzzled. Being a bit of a show-off at that time, I raised my hand and went up in front of the class to explain. I am not sure if anyone understood what I was trying to say but here is what I said:

Using modular arithmetic, it is not difficult to show that the remainder of a number on division by 9 is the same as the remainder of the sum of the digits of the number on division by 9. Indeed, writing an integer in the natural base 10 representation, we have:

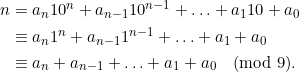
Now, if the digits in a number are written in a different order, then notice that this does not affect the sum of the digits. Thus, by the above, two such numbers leave the same remainder on division by 9. Hence, their difference is divisible by 9. For example, if 6758 is mistakenly written as 6578, then the difference is 180 which is of course divisible by 9. This explains the above statement in quotations that if the difference happens to be divisible by 9 then it might be caused by a transposition of the digits.

Obviously, transposition of digits is not the only cause. It might also be from multiple data entry errors or if someone writes 90 instead of 99. In any case, this is an interesting application of modular arithmetic in accounting.