The Twelve Days of Christmas

on January 26, 2024

This post is inspired by the well-known Christmas song "The Twelve Days of Christmas", which starts as follows:

"On the first day of Christmas,
my true love gave to me
A partridge in a pear tree.

On the second day of Christmas,
my true love gave to me
Two turtle doves,
And a partridge in a pear tree."

A natural mathematical question related to this song is how many gifts in total did my true love give to me.

Essentially, the answer is the sum of the first twelve triangular numbers, where the $n$ -th triangular number is defined as the sum of all integers from $1$ to $n$ . Recall from my earlier post "The genius of Gauss" that the sum of the first $n$ integers is $n(n+1)/2$ . So using this formula, one can determine the answer by writing down the first twelve triangular numbers and adding them up.

I want to generalize the situation and find the sum if the song is "The $N$ days of Christmas". How many gifts did my true love give to me in this case? Of course, the answer depends on $N$ . I would like to develop the formula in this post. Clearly, the sum can be written as

$\sum_{n=1}^N \frac{n(n+1)}{2}.$

But how do we calculate this sum? Note that

$\sum_{n=1}^N \frac{n(n+1)}{2} = \frac{1}{2}\big(\sum_{n=1}^N n^2 + \sum_{n=1}^N n \big) .$

Thus, the question boils down to finding the expression for the sum of the first $N$ squares and the sum of the first $N$ integers. Since we know the latter, we devote our attention to finding the sum of the first $N$ squares.

Recall the general identity $(n+1)^3=n^3+3n^2+3n+1$ or equivalently

$n^2=\frac{1}{3}\big((n+1)^3-n^3\big)-n-\frac{1}{3}.$

We get $N$ such equations if we replace $n$ successively from $1$ to $N$ . Summing these $N$ equations yield:

$\begin{align*} \sum_{n=1}^N n^2 &= \frac{1}{3}\sum_{n=1}^N \big((n+1)^3-n^3\big) - \sum_{n=1}^N n- \sum_{n=1}^N \frac{1}{3} \\ &= \frac{1}{3} \big((N+1)^3-1\big)- \frac{N(N+1)}{2} - \frac{N}{3} \\ &= \frac{1}{6} \big(2(N+1)^3-2-3N(N+1)-2N \big) \\ &= \frac{1}{6} (2N^3+3N^2+N) \\ &= \frac{N(N+1)(2N+1)}{6}. \end{align*}$

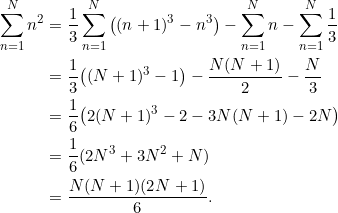
Thus, the number of gifts my true love gave to me in "The $N$ days of Christmas" is:

$\begin{align*} \sum_{n=1}^N \frac{n(n+1)}{2}&=\frac{1}{2}\big(\sum_{n=1}^N n^2 + \sum_{n=1}^N n \big) \\ &=\frac{1}{2}\big(\frac{N(N+1)(2N+1)}{6}+\frac{N(N+1)}{2}\big) \\ &=\frac{N(N+1)}{4}\big(\frac{2N+1}{3}+1\big) \\ &=\frac{N(N+1)}{4}\big(\frac{2N+4}{3}\big) \\ &=\frac{N(N+1)(N+2)}{6}. \end{align*}$

In particular, when $N=12$ , I get $12(13)(14)/6=364$ gifts.

Categories:

Mathematics

Tags:

No Tag

Comments are closed